【人気ダウンロード!】 色々な立体の体積 151480

小5 複雑な立体の体積 直方体 日本語版 Youtube
・透明なので,立体の構造が把握しやすい ・展開図が理解できる ・必要最小限のパーツが付属している 物足りない点 ・どちらかと言うと家庭向け 複雑な立体には不適 ・パーツが少ないように感じた ・中学受験高学年向けではない ・灘中で出題されるような立体の展開図には対応していないこの立体の体積を求めよ。 12cm 12cm 8cm 4cm 次の平面図形をそれぞれ直線mを軸として1回転させてできる回転体の体積を求めよ。 6cm 3cm 10cm m ① m 6cm 8cm ② ③ m 3cm 2cm 10cm pdfファイル 解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。 解説リクエスト 解説
色々な立体の体積
色々な立体の体積- 平面 z = t で切った切り口の面積が分かれば,所謂「薄切りハムの体積」が分かったようなものだから,立体全体の体積も計算できるね。 (2)の解答 題意の部分を平面 z = t で切った切り口の面積は (1)より 4 ( 1 − t 2) だから,求める体積は ∫ − 1 1 4 ( 1 − t 2) d t = 8 ∫ 0 1 ( 1 − t 2) d t = 8 t − 1 3 t 3 0 1 = 16 3 (3)の考え方と解答3円柱の共通部分の体積けることによって色々な柱状体積を求めることができるようにすることをねらいとしている。 本単元における既習事項は、直方体と立方体の体積の求め方である。その中でも「高さを1cm に切った立体の体積をまず考え、その体積を高さの分だけ倍にする考え方」がその基となる。この 考え方を

6年生算数ドリル 立体
体積の意味って? 体積は簡単に言ってしまえば、立体の大きさのことで、単位は cm3 c m 3 や m3 m 3 を使います。 立方体や直方体の体積の求め方を、体積の単元の序盤に習うと思います。 そのとき使う単位だと考えればOKです。 一方で、水や牛乳のような液体を計るときに使う単位は色々なものがあります。 体積と同じように cm3 c m 3 や m3 m 3 を使うこともありますいろいろな立体の問題 ここでは,体積を中心にいろいろな立体の問題を扱います. 目次は次の通りです. いろいろな立体の問題 第1節 体積における置換積分を身につけよう 体積における置換積分を身につけよう(その1) 体積における置換積分を身につけよう(その2) 体積における置換積分を身につけよう(その3) 体積における置換積分を身につけよう(その4)体積の計算式は「半径×半径×円周率×高さ」です。 幾何学の問題では、円周率の値が細かく指定されていることもありますが、ほとんどの場合、314を用いれば充分でしょう。 念のため、担当の教師に用いるべき値を確認しておくと安心です。 円柱の体積
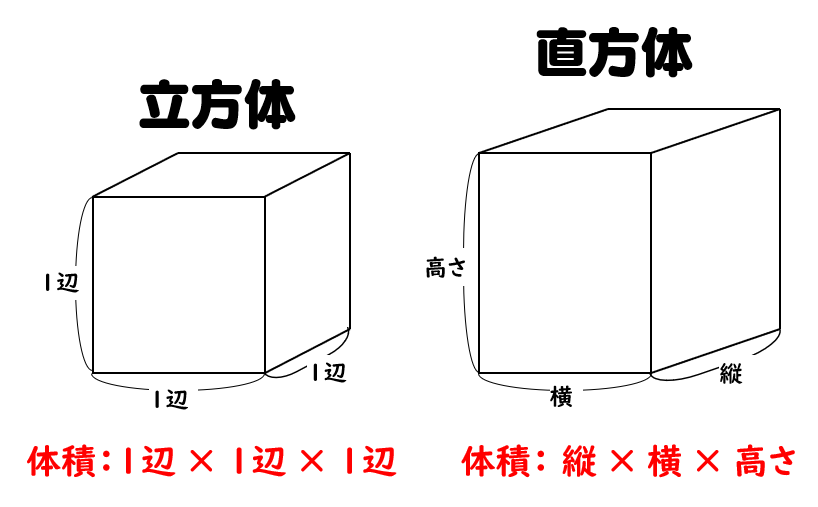
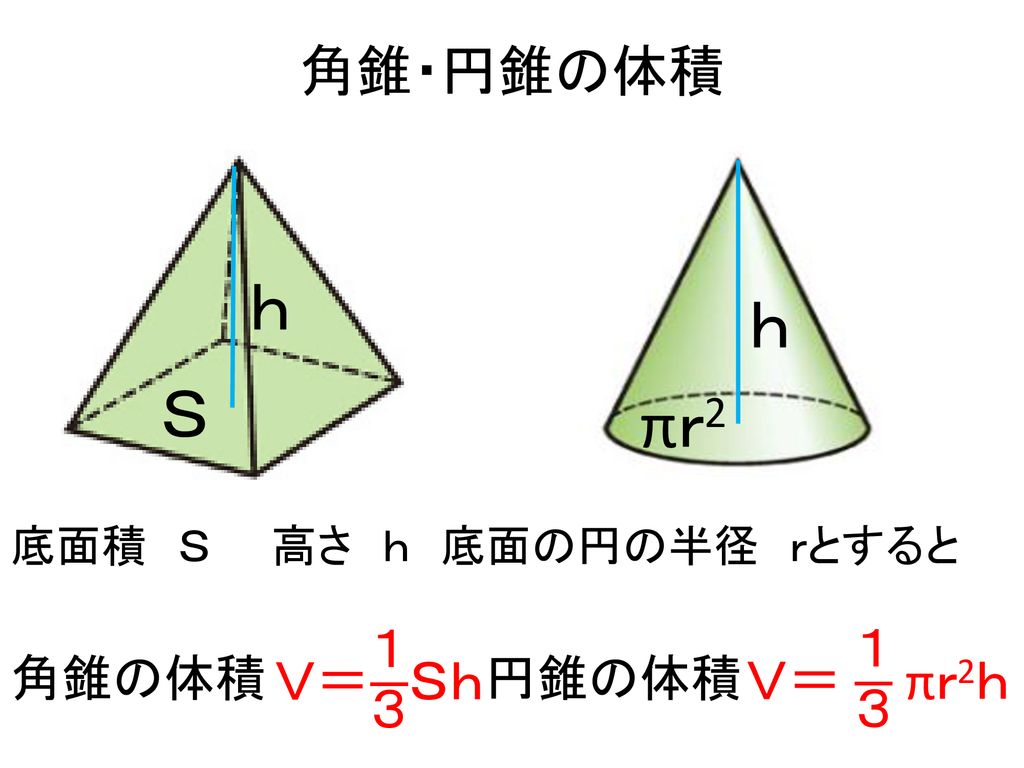
立方体の12の辺の長さは等しく、これを $a$ とします。立方体の体積 $V$ は、次の式で求められます。 立方体 (りっぽうたい) の体積 \begin{align*} V = a^3 \end{align*} 体積 = 一辺 × 一辺 × 一辺 意外と色々な立体の面積や体積の求め方について記載されている本は少ないですよね。 私は「機械工学必携」 (昭和49年発行 (めちゃ古いですね (^_^)、三省堂発刊,900ページ余りの割合コンパクトな本です)を重宝して使っています。 確かこの発行所は今は無くなったかとは思いますが。 三角形の面積から球冠、球帯、球分、回転楕円体、回転放物帯などの 錐体(円錐、角錐)の体積は、底面積が S S 、高さが h h の錐体の体積 V V は以下の式で表します。 V = 1 3Sh V = 1 3 S h この公式を学習したときに 1 3 1 3 になる理由は知らなかったと思います。 これは特殊な四角錐の場合には比を用いて簡単に証明することが
色々な立体の体積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「色々な立体の体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
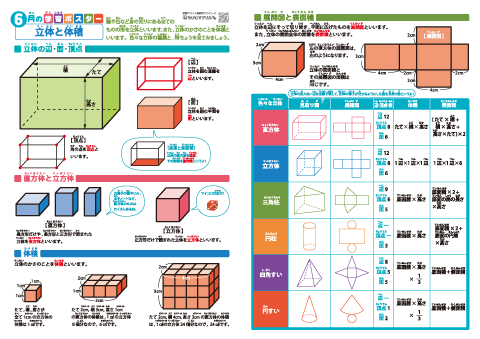 |  |
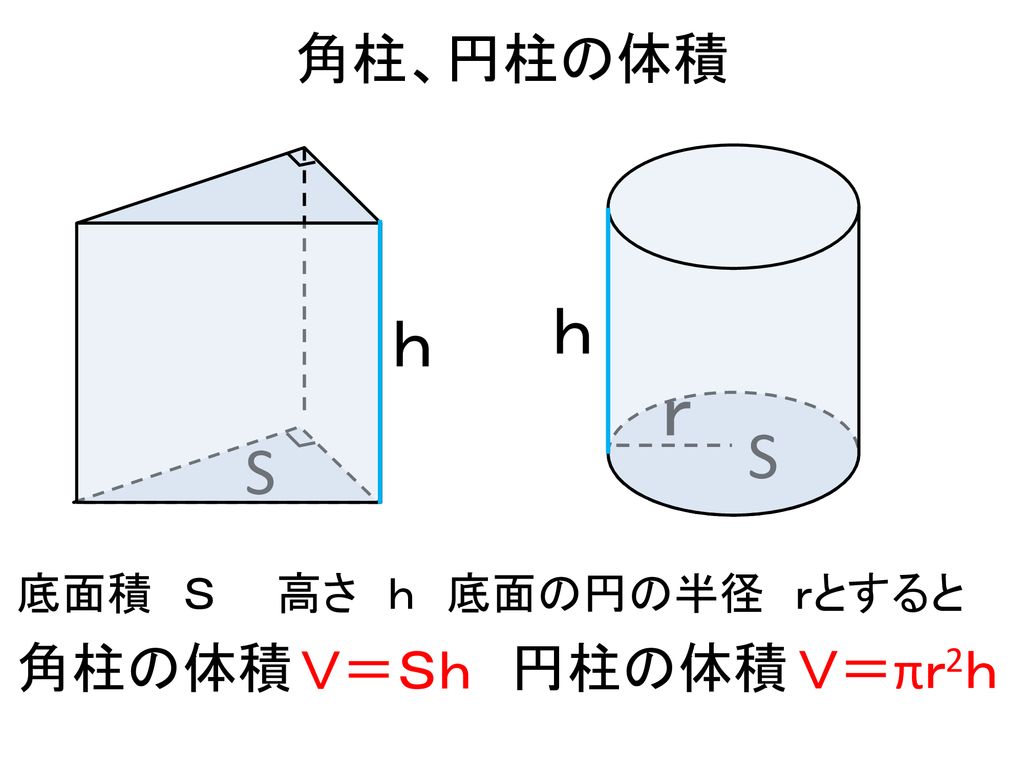
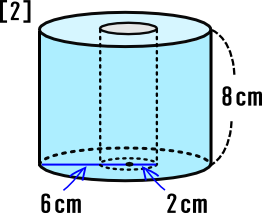
立方体や直方体、そして円柱のような立体の体積はすべて、(底面の面積)×(底面を面と垂直方向に平行移動させた距離)を計算することで求まります。 したがって、上図のような斜円柱の体積の求め方も直円柱同様に、 $ V=Sh $ で求めることが出来ます。ここで、高さ h は2つの底面間の距離表面積や体積の求め方 (三角柱,四角柱,円柱,球や半球) 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。
コメント
コメントを投稿